Функция проверки Excel Z
Excel Z TEST - это своего рода проверка гипотез, которая используется для проверки альтернативной гипотезы против нулевой гипотезы. Нулевая гипотеза - это гипотеза, которая относится к общему утверждению в целом. Путем проверки гипотезы мы пытаемся доказать, что нулевая гипотеза ложна против альтернативной гипотезы.
Z-ТЕСТ - одна из таких функций проверки гипотез. Это проверяет среднее значение двух наборов данных выборки, когда дисперсия известна и размер выборки большой. Размер выборки должен быть> = 30, иначе нам нужно использовать T-TEST. Для ZTEST нам нужно иметь две независимые точки данных, которые не связаны друг с другом или не влияют друг на друга, и данные должны быть нормально распределены.
Синтаксис
Z.TEST - это встроенная функция в Excel. Ниже приведена формула функции Z.TEST в excel.

- Массив: это диапазон ячеек, содержащий точки данных, по которым нам нужно проверить X. Это значение ячеек по сравнению со средним значением выборки гипотез, которое необходимо проверить.
- X: Из массива проверяемое значение X.
- Сигма: это стандартное отклонение для всего населения. Это необязательный аргумент, если он не указан, используйте стандартное отклонение образца.
Как выполнить тест Z в Excel? (с примерами)
Вы можете скачать этот шаблон Excel Z Test здесь - Шаблон Z Test ExcelПример # 1 - Использование формулы Z-теста
Например, посмотрите на данные ниже.
Используя эти данные, мы рассчитаем одностороннее значение вероятности Z TEST. Для этого предположим, что среднее значение гипотезы равно 6.
- Шаг 1. Итак, откройте формулу Z TEST в ячейке Excel.
- Шаг 2: Выберите массив в качестве баллов, то есть от A2 до A11.
- Шаг 3: Следующий аргумент - «X» . Поскольку мы уже предположили, что предполагаемое среднее значение совокупности равно 6, примените это значение к этому аргументу.
- Шаг 4. Последний аргумент является необязательным, поэтому закройте формулу, чтобы получить значение Z TEST.
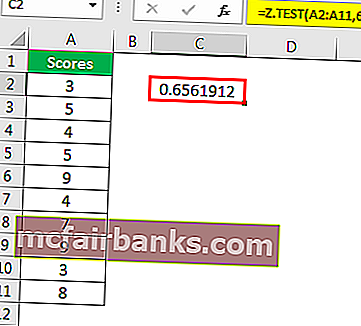
- Шаг 5: Это одностороннее значение Z TEST, чтобы получить двустороннее значение Z TEST для умножения этого значения на 2.
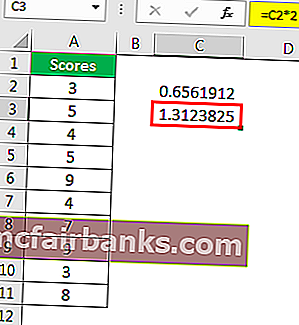
Пример # 2 - Z-ТЕСТ с использованием опции анализа данных
Мы можем провести Z TEST, используя опцию анализа данных в Excel. Чтобы сравнить два средних значения, когда дисперсия известна, мы используем Z TEST. Здесь мы можем сформулировать две гипотезы, одна - «Нулевая гипотеза», а другая - «Альтернативная гипотеза», ниже приводится уравнение обеих этих гипотез.
H0: μ1 - μ2 = 0 (нулевая гипотеза)
H1: μ1 - μ2 ≠ 0 (альтернативная гипотеза)
Альтернативная гипотеза (H1) утверждает, что два средних значения совокупности не равны.
В этом примере мы будем использовать результаты двух учеников по нескольким предметам.
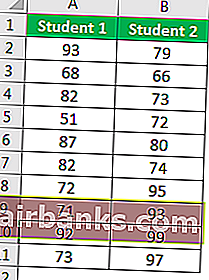
- Шаг 1: Первое, что нам нужно сделать, это вычислить переменные для этих двух значений с помощью функции VAR.P.
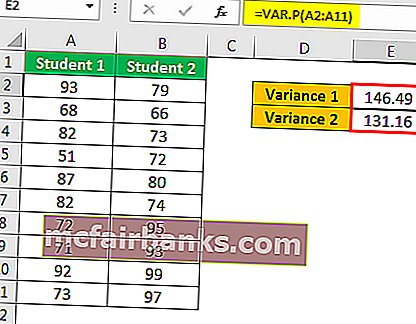
- Шаг 2: Теперь перейдите на вкладку «Данные» и нажмите «Анализ данных».

Прокрутите вниз и выберите z-Test Two Sample для средних и нажмите Ok.
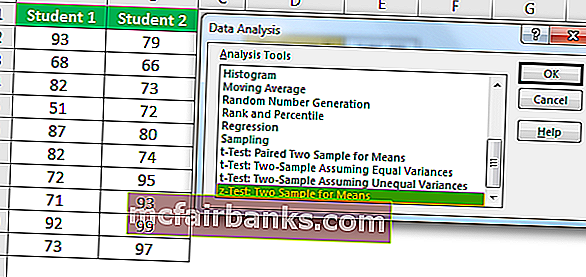
- Шаг 3. Для диапазона переменной 1 выберите баллы «Студент 1», а для диапазона переменной 2 выберите баллы «Студент 2».
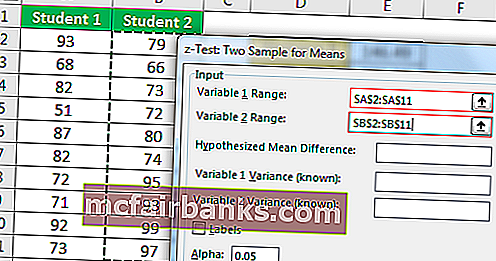
- Шаг 4: Переменная 1 Дисперсия выберите Оценка дисперсии учащегося 1 и Переменная 1 Дисперсия выберите Оценка дисперсии учащегося 2.
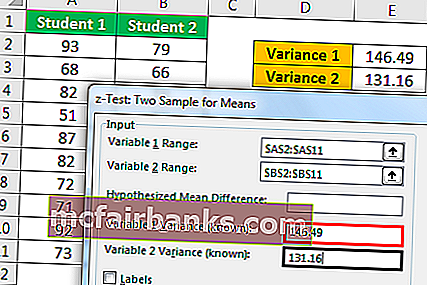
- Шаг 5: Выберите диапазон вывода в качестве ячейки и нажмите ОК.
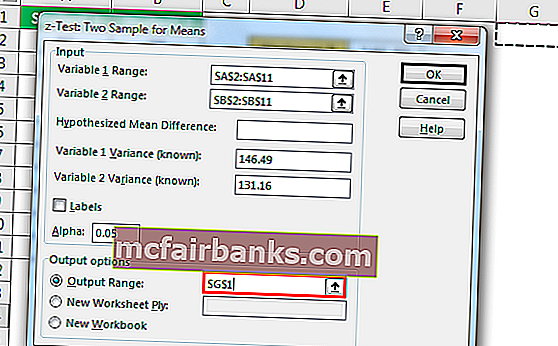
мы получили результат.
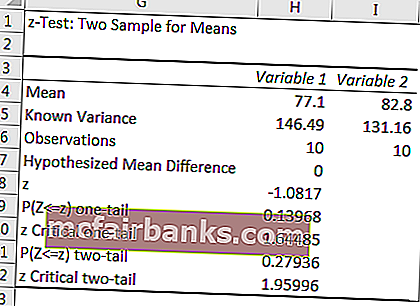
Если Z <- Z Critical Two Tailor Z> Z Critical Two Tail, то мы можем отклонить нулевую гипотезу.
Итак, из результата ZTEST ниже приведены результаты.
- Z <- Z Критический два хвоста = -1,080775083> - 1,959963985
- Z> Z Критический двуххвостый = -1,080775083 <1,959963985
Поскольку он соответствует нашим критериям, мы не можем отклонить нулевую гипотезу. Таким образом, средства двух учеников существенно не различаются.
То, что нужно запомнить
- Все аргументы должны иметь числовые значения, иначе мы получим # ЗНАЧЕНИЕ !.
- Значение массива должно содержать числа, иначе мы получим ошибку # N / A.
- ZTEST можно применять к большим наборам данных.